How to Draw Vectors on X Y Plane

Vectors

This is a vector:

A vector has magnitude (size) and direction:

The length of the line shows its magnitude and the arrowhead points in the direction.

Nosotros tin add two vectors past joining them head-to-tail:

And it doesn't matter which order we add them, we go the same effect:

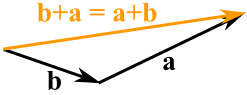
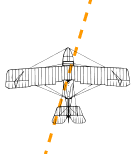
Example: A plane is flying along, pointing N, merely there is a wind coming from the North-West.

The 2 vectors (the velocity acquired by the propeller, and the velocity of the wind) result in a slightly slower ground speed heading a little East of N.

If you watched the airplane from the ground it would seem to exist slipping sideways a little.

Have yous ever seen that happen? Mayhap you have seen birds struggling confronting a strong air current that seem to fly sideways. Vectors assistance explain that.

Velocity, dispatch, strength and many other things are vectors.

Subtracting

We tin can likewise subtract one vector from another:

• first we reverse the direction of the vector nosotros want to subtract,
• and then add them as usual:

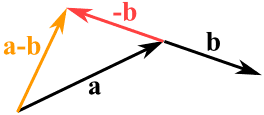
a − b

Notation

A vector is often written in assuming, like a or b.

A vector can also be written as the messages of its head and tail with an arrow above it, like this:

Calculations

Now ... how do nosotros do the calculations?

The near common mode is to first suspension up vectors into x and y parts, like this:

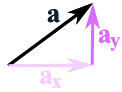
The vector a is broken up into
the two vectors a_ten and a_y

(We run across later how to practise this.)

Adding Vectors

We tin can then add together vectors by adding the x parts and adding the y parts:

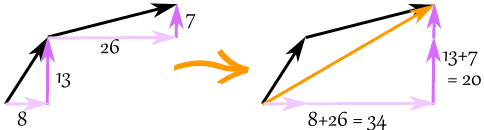
The vector (8, xiii) and the vector (26, seven) add upwardly to the vector (34, twenty)

Example: add the vectors a = (8, xiii) and b = (26, 7)

c = a + b

c = (8, xiii) + (26, 7) = (8+26, 13+7) = (34, 20)

When we break upward a vector like that, each office is called a component:

Subtracting Vectors

To decrease, showtime reverse the vector we want to subtract, and then add.

Case: subtract thousand = (4, 5) from 5 = (12, 2)

a = v + −thousand

a = (12, 2) + −(4, 5) = (12, ii) + (−iv, −5) = (12−4, two−5) = (8, −3)

Magnitude of a Vector

The magnitude of a vector is shown by 2 vertical bars on either side of the vector:

|a|

OR it can exist written with double vertical bars (and so as not to misfile it with absolute value):

||a||

We use Pythagoras' theorem to summate it:

|a| = √( 10² + yⁱⁱ )

Example: what is the magnitude of the vector b = (6, eight) ?

|b| = √( 6² + 8²) = √( 36+64) = √100 = 10

A vector with magnitude 1 is called a Unit Vector.

Vector vs Scalar

A scalar has magnitude (size) only.

Scalar: simply a number (like 7 or −0.32) ... definitely not a vector.

A vector has magnitude and direction, and is often written in bold, so we know it is not a scalar:

• so c is a vector, it has magnitude and direction
• but c is just a value, like 3 or 12.four

Example: kb is actually the scalar chiliad times the vector b.

Multiplying a Vector past a Scalar

When we multiply a vector by a scalar it is called "scaling" a vector, considering we change how big or small the vector is.

Example: multiply the vector m = (7, three) by the scalar 3

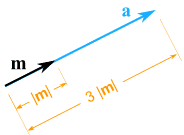a = threethou = (three×7, 3×3) = (21, 9)

It nonetheless points in the same direction, but is iii times longer

(And now you know why numbers are called "scalars", because they "scale" the vector up or downward.)

Multiplying a Vector by a Vector (Dot Product and Cross Product)

How do we multiply two vectors together? In that location is more ane way! The scalar or Dot Product (the result is a scalar). The vector or Cross Production (the result is a vector). (Read those pages for more details.)

More Than 2 Dimensions

Vectors likewise piece of work perfectly well in three or more dimensions:

The vector (i, 4, v)

Example: add the vectors a = (3, 7, 4) and b = (2, ix, 11)

c = a + b

c = (3, 7, 4) + (ii, ix, 11) = (iii+2, 7+9, 4+11) = (5, 16, 15)

Instance: what is the magnitude of the vector due west = (1, −two, 3) ?

|w| = √( 1² + (−two)^two + 3² ) = √( i+4+9) = √xiv

Here is an case with iv dimensions (only it is hard to draw!):

Case: subtract (1, 2, 3, four) from (3, 3, 3, 3)

(3, 3, iii, 3) + −(i, 2, three, 4)
= (3, 3, iii, 3) + (−ane,−2,−three,−4)
= (3−1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)

Magnitude and Direction

Nosotros may know a vector's magnitude and direction, but want its x and y lengths (or vice versa):

Y'all tin read how to convert them at Polar and Cartesian Coordinates, but here is a quick summary:

From Polar Coordinates (r,θ) to Cartesian Coordinates (x,y)		From Cartesian Coordinates (x,y) to Polar Coordinates (r,θ)
10 = r × cos( θ ) y = r × sin( θ )		r = √ ( x2 + y2 ) θ = tan-i ( y / x )

An Example

Sam and Alex are pulling a box.

• Sam pulls with 200 Newtons of forcefulness at 60°
• Alex pulls with 120 Newtons of force at 45° as shown

What is the combined force, and its direction?

Permit us add the 2 vectors head to tail:

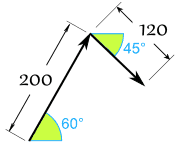
First convert from polar to Cartesian (to 2 decimals):

Sam's Vector:

• x = r × cos( θ ) = 200 × cos(sixty°) = 200 × 0.5 = 100
• y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21

Alex's Vector:

• 10 = r × cos( θ ) = 120 × cos(−45°) = 120 × 0.7071 = 84.85
• y = r × sin( θ ) = 120 × sin(−45°) = 120 × -0.7071 = −84.85

Now we have:

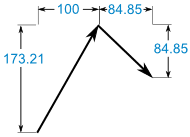
Add together them:

(100, 173.21) + (84.85, −84.85) = (184.85, 88.36)

That reply is valid, but allow's catechumen back to polar as the question was in polar:

• r = √ ( x² + y² ) = √ ( 184.85² + 88.36² ) = 204.88
• θ = tan^-1 ( y / ten ) = tan^-1 ( 88.36 / 184.85 ) = 25.5°

And we have this (rounded) effect:

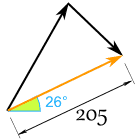
And information technology looks like this for Sam and Alex:

They might get a better consequence if they were shoulder-to-shoulder!

minesmaidne.blogspot.com

Source: https://www.mathsisfun.com/algebra/vectors.html

Share this post